Last Updated:
By Adam Cunningham and John Ringland

Trios Pitagóricos e a Geometria Aritmética

Trios Pitagóricos Densos: Uma Jornada Fascinante pela Geometria Aritmética

A proposição dos trios Pitagóricos densos apresenta conexões interessantes entre geometria e teoria dos números, monstrando que problemas simples podem revelar elaboradas propriedades matemáticas. Expandimos aqui o texto do Chris Grossack, não apenas o problema central, mas também algumas aplicações e métodos de visualização.

O trio de números inteiros \( \{a, b, c\} \) é Pitagórico se $$a^2 + b^2 = c^2.$$

Exemplos famosos são

  • {3, 4, 5}
  • {5, 12, 13}
  • {7, 24, 25}
  • {8, 15, 17}

Os trios {0,0,0}, \( \{0, b, b\} \) e \(\{a, 0, a\}\) são casos triviais \(\forall a \) e \( \forall b \in \mathbb{Z} \).

O problema e sua solução geométrica

A questão central que inspirou esta exploração é aparentemente simples:

Sejam \(\alpha\) e \(\beta \) dois números racionais com $$0 < \alpha < \beta < 1.$$ Para qualquer par \( (\alpha, \beta) \) existe sempre um trio Pitagórico \(\{a, b, c\}\) com $$\alpha < \frac{a}{b} < \beta ?$$

A resposta é sim. É este o sentido de “densidade” – \(a/b\) “ocupa” o espaço do intervalo entre \(\alpha\) e \(\beta\). No mesmo sentido que os números racionais são densos no conjunto dos números reais.

A demonstração utiliza uma técnica de geometria aritmética que transforma o problema algébrico em um problema geométrico. Reescrevendo \(a^2 + b^2 = c^2\) como $$\left( \frac{a}{c} \right)^2 + \left( \frac{b}{c} \right)^2 = 1,$$ mapeamos os trios Pitagóricos nos pares de números racionais \( (u, v) = (a/c, b/c) \) que por sua vez correspondem bijetivamente a pontos racionais no círculo unitário. Esta correspondência é a chave para responder a pergunta.

A elegância da solução reside na projeção estereográfica: partindo do ponto \( (-1,0) \) no círculo unitário, qualquer reta com inclinação racional \( t \) intersecta o círculo em exatamente um outro ponto racional. Inversamente, qualquer ponto racional no círculo (exceto (-1,0)) determina uma linha com inclinação racional através de \( (-1,0) \).

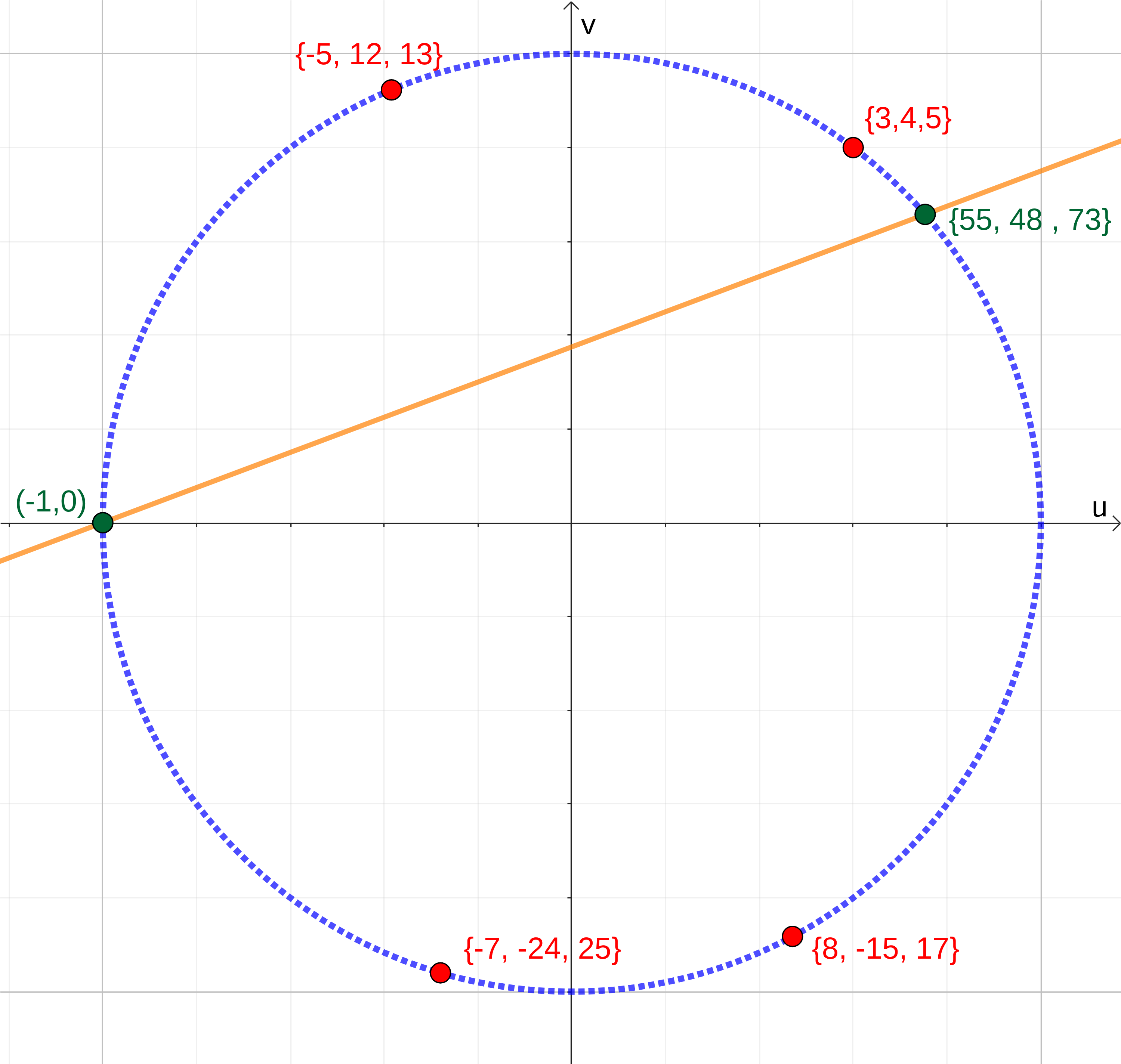
picture
Círculo unitário e a projeção estereográfica pela reta \( v = t (u+1) \) no plano \( (u, v)\) . Na imagem alguns trios estão representados. A reta em exibição tem inclinação dada por \(t = 3/8 \).

Reformulação via hipérbole e a resposta completa

O problema original questiona sobre \(a/b\), então é natural reformular o problema usando a hipérbole $$y^2 - x^2 = 1$$ em que \(x = a/b\) e \(y = c/b\). A partir do ponto óbvio (0,1) nesta hipérbole, podemos gerar todos os pontos racionais através de retas \(y=1+s x\) de inclinação racional \(s \in (-1,1)\).

A parametrização explícita dos pontos no ramo positivo da hipérbole é $$P =\left( x(s), y(s) \right) = \left(\frac{2 s}{1-s^2}, \frac{1+s^2}{1-s^2}\right),$$

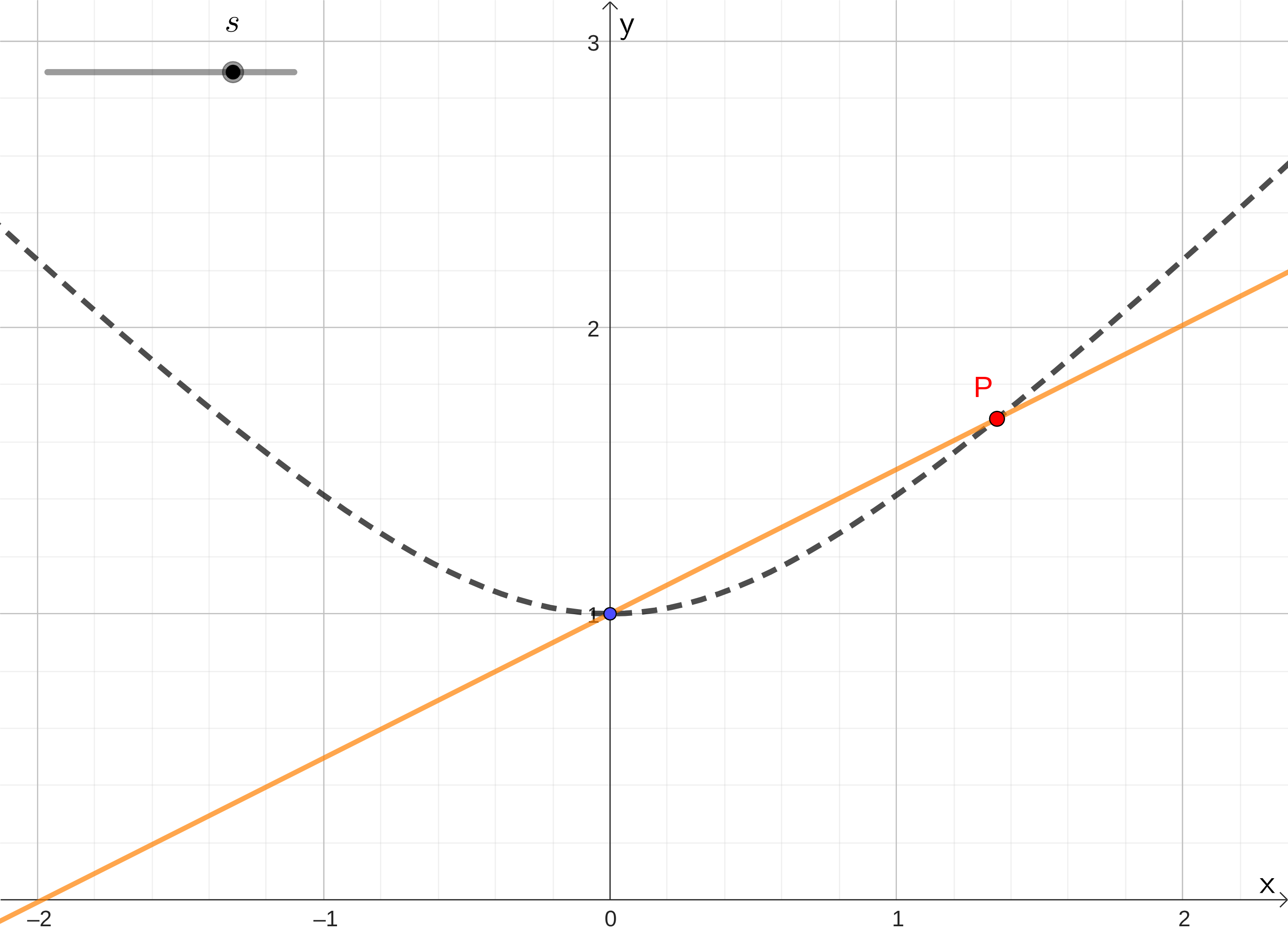
picture
Ramo \(y>0\) da hipérbole e a reta \(y=1+s x\) de inclinação racional \(s \in (-1,1)\) intercepta a hipérbole exatamente em um ponto racional \(P\).

A função \(x(s) \) aumenta monotonicamente de \(-\infty \) para \(+\infty \) quando \(s \) vai de \(-1\) para \(+1 \), garantindo que para qualquer intervalo \((\alpha, \beta) \), podemos encontrar valores de \(s \) que produzem pontos racionais com coordenada \(x \) no intervalo desejado. A função inversa $$s(x) = \frac{\sqrt{1 + x^2} -1}{x}$$ permite calcular esses valores. Isto é $$ \frac{\sqrt{1 + \alpha^2} -1}{\alpha} < s < \frac{\sqrt{1 + \beta^2} -1}{\beta} $$ garante que existe \(\alpha < x < \beta \)!

**Exercício:

*Encontre um trio Pitagórico com \( 3/7< a/b <4/7 \) usando a fórmula de \(s \).

Propriedades matemáticas e densidade

Densidade assintótica de Lehmer

A D.H. Lehmer é creditata uma demonstração de que a quantidade de trios Pitagóricos primitivos (\(a\) e \(b\) coprimos) com hipotenusa \(c\) menor que \(h\) é assintoticamente $$\frac{h}{2 \pi} \approx 0.159 h.$$ Isto é, aproximadamente 15,9% dos números inteiros participam como hipotenusas de trios Pitagóricos primitivos.

Fórmula de Euclides e estrutura paramétrica

Euclides forneceu uma parametrização de trios Pitagóricos primitivos: para numéros naturais \( k > ℓ > 0 \) em que MDC\( (k,ℓ) = 1\) e \(k- ℓ \) é par: $$ a = k^2 - ℓ^2 \quad b = 2 k ℓ \Rightarrow c = k^2 + ℓ^2 $$

Esta fórmula revela que trios Pitagóricos primitivos formam uma estrutura em árvore ternária infinita com propriedades fractais.

Visualização com Geogebra e implementação em Python

Geogebra

As figuras acima fora geradas com o Geogebra de forma bastante intuitiva. Veja

Geração de trios Pitagóricos e cálculo da densidade com Python

#!/usr/bin/env python3
"""
Geração e análise de trios pitagóricos até um limite de hipotenusa.
Inclui:
- Geração de trios primitivos (fórmula de Euclides)
- Geração de trios primitivos e múltiplos opcionais
- Formatação tabular da lista de trios
- Cálculo e relatório de densidade observada vs. teórica
"""

import math
from typing import Iterator, Tuple, List

# ---------------------------------------------------------------------
# 1. Geração de trios pitagóricos
# ---------------------------------------------------------------------

def generate_primitive_triples(limit: int) -> Iterator[Tuple[int, int, int]]:
    """
    Gera trios pitagóricos PRIMITIVOS (a, b, c) com c <= limit,
    usando a fórmula de Euclides:
      a = m² – n²,  b = 2·m·n,  c = m² + n²
    """
    m = 2
    while m * m + 1 <= limit:
        for n in range(1, m):
            if (m - n) % 2 == 1 and math.gcd(m, n) == 1:
                a = m*m - n*n
                b = 2*m*n
                c = m*m + n*n
                if c <= limit:
                    yield (a, b, c)
        m += 1

def generate_triples(
    limit: int,
    include_multiples: bool = False
) -> Iterator[Tuple[int, int, int]]:
    """
    Gera trios pitagóricos (primitivos e, opcionalmente, seus múltiplos)
    com hipotenusa c <= limit.
    
    :param limit: valor máximo para c
    :param include_multiples: inclui k·(a,b,c) para k>=2
    """
    for a, b, c in generate_primitive_triples(limit):
        yield (a, b, c)
        if include_multiples:
            k = 2
            while k * c <= limit:
                yield (k*a, k*b, k*c)
                k += 1

# ---------------------------------------------------------------------
# 2. Formatação da lista de trios
# ---------------------------------------------------------------------

def format_triples(
    triples: Iterator[Tuple[int, int, int]]
) -> str:
    """
    Converte um iterável de trios em uma string tabular,
    com colunas alinhadas.
    """
    rows = sorted(triples, key=lambda t: t[2])
    if not rows:
        return "Nenhum trio encontrado."
    
    header = f"{'a':>5s} {'b':>5s} {'c':>5s}"
    sep    = "-" * len(header)
    lines  = [header, sep]
    for a, b, c in rows:
        lines.append(f"{a:5d} {b:5d} {c:5d}")
    return "\n".join(lines)

# ---------------------------------------------------------------------
# 3. Análise de densidade
# ---------------------------------------------------------------------

def calculate_densities(
    primitive_triples: List[Tuple[int, int, int]],
    limit: int
) -> Tuple[float, float]:
    """
    Retorna (densidade_observada, densidade_teórica),
    onde:
      densidade_observada = N_primitivas / limit
      densidade_teórica = 1 / (2·π)
    """
    observed    = len(primitive_triples) / limit
    theoretical = 1 / (2 * math.pi)
    return observed, theoretical

def format_density_report(
    limit: int,
    primitive_count: int,
    observed: float,
    theoretical: float
) -> str:
    """
    Gera relatório formatado de densidade, com:
      - número de triplas
      - densidade observada
      - densidade teórica
      - diferença relativa (%)
    """
    rel_diff = abs(observed - theoretical) / theoretical * 100
    header   = f"Análise de Densidade (c ≤ {limit})"
    sep      = "-" * len(header)
    body     = (
        f"Triplas primitivas encontradas : {primitive_count}\n"
        f"Densidade observada            : {observed:.6f}\n"
        f"Densidade teórica              : {theoretical:.6f}\n"
        f"Diferença relativa             : {rel_diff:.2f}%"
    )
    return f"{header}\n{sep}\n{body}"

def analyze_density(limit: int = 10000) -> Tuple[List[Tuple[int, int, int]], float]:
    """
    Executa todo o fluxo de análise de densidade:
      1. Gera trios primitivos até 'limit'
      2. Calcula densidades observada e teórica
      3. Imprime relatório
    Retorna (lista_de_primitivas, densidade_observada).
    """
    primitives = list(generate_primitive_triples(limit))
    observed, theoretical = calculate_densities(primitives, limit)
    report = format_density_report(limit, len(primitives), observed, theoretical)
    print(report)
    return primitives, observed

# ---------------------------------------------------------------------
# 4. Função principal
# ---------------------------------------------------------------------

def main():
    # Parâmetros de exemplo 
    include_multiples = False

    # 1) Exibe tabela de trios
        limit = 158
    print(f"Trios pitagóricos (c ≤ {limit}):\n")
    print(format_triples(generate_triples(limit, include_multiples)))
    print()

    # 2) Executa análise de densidade
        limit = 10000
    analyze_density(limit)

if __name__ == "__main__":
    main()

A saída deste script é:

Trios pitagóricos (c ≤ 158):

    a     b     c
-----------------
    3     4     5
    5    12    13
   15     8    17
    7    24    25
   21    20    29
   35    12    37
    9    40    41
   45    28    53
   11    60    61
   33    56    65
   63    16    65
   55    48    73
   13    84    85
   77    36    85
   39    80    89
   65    72    97
   99    20   101
   91    60   109
   15   112   113
  117    44   125
  105    88   137
   17   144   145
  143    24   145
   51   140   149
   85   132   157

Esta saída lista 25 trios Pitagóricos. Que é o valor estimado por Lehmer para \(h=158 \), isto é, \(158/(2 \pi) \approx 25 \).

E a outra saída para \(h=10000 \) é:

Análise de Densidade (c ≤ 10000)
--------------------------------
Triplas primitivas encontradas : 1593
Densidade observada            : 0.159300
Densidade teórica              : 0.159155
Diferença relativa             : 0.09%

Este cálculo reforça a estimativa de Lehmer.

Aplicações modernas e relevância contemporânea

Criptografia e segurança

Propriedades criptográficas dos trios Pitagóricos estão sendo exploradas em pesquisas modernas. Subhash Kak descobriu que triplas primitivas podem ser classificadas em seis classes distintas, cada uma com propriedades estatísticas únicas adequadas para geração de chaves criptográficas.

Computação gráfica e jogos

Na computação gráfica, trios Pitagóricos permitem cálculos exatos de distâncias sem aproximações decimais, cruciais para detecção de colisões, renderização de gráficos e criação de movimentos realistas em ambientes virtuais.

Aprendizado de máquina e ciência de dados

O teorema de Pitágoras estende-se para dimensões superiores como a fórmula de distância euclidiana, fundamental para algoritmos de agrupamento, buscas por vizinhos mais próximos e técnicas de redução de dimensionalidade.

Construção e arquitetura

O método do triângulo 3-4-5 continua sendo usado por construtores modernos para criar ângulos retos perfeitos, garantindo cantos quadrados, paredes perpendiculares e fundações precisas.

Extensões e generalizações

Quádruplas e n-uplas pitagóricas

Quádruplas pitagóricas \( {a,b,c,d}\) satisfazem \( a^2 + b^2 + c^2 = d^2 \), representando caixas retangulares com comprimentos laterais inteiros e diagonal espacial inteira. Exemplos incluem {1,2,2,3} e {2,3,6,7}.

Extensões n-dimensionais conectam-se à cristalografia, geometria superior e física teórica.

Teoria dos números algébricos

As triplas conectam-se à teoria dos números algébricos através de inteiros gaussianos, curvas elípticas e formas modulares, demonstrando como conceitos elementares podem levar a matemática avançada.

Considerações pedagógicas

trios Pitagóricos oferecem uma ponte entre matemática básica e teoria abstrata, permitindo que estudantes experimentem com números específicos enquanto descobrem padrões gerais.

O reconhecimento de padrões emerge ao explorar trios sistematicamente, desenvolvendo intuição matemática.

Programação e visualização reforçam conceitos abstratos, permitindo exploração interativa, impossível com apenas lápis e papel.

Conclusão e perspectivas futuras

A beleza das trios Pitagóricos está na convergência de múltiplas áreas matemáticas: geometria, álgebra, teoria dos números e análise. O problema aparentemente simples sobre densidade revela conexões entre diferentes ramos da matemática.

A equivalência biracional entre o círculo unitário e a linha afim exemplifica como pensamento geométrico pode resolver problemas algébricos, enquanto a parametrização explícita fornece ferramentas computacionais práticas. Há uma estudos que conectando os trios Pitagóricos à geometria não-comutativa.

As aplicações modernas - desde criptografia até aprendizado de máquina - demonstram que conceitos matemáticos fundamentais mantêm relevância contemporânea. A estrutura em árvore das triplas primitivas continua revelando padrões e propriedades, prometendo descobertas futuras.

Para estudantes e entusiastas da matemática, trios Pitagóricos oferecem um laboratório para explorar como matemática elementar se conecta a conceitos avançados, que podem revelar surpresas quando examinados com ferramentas contemporâneas.

Referências

Fonte Principal

Grossack, Chris (2021). “Dense Pythagorean Triples – A Cute Problem in Arithmetic Geometry”. Chris Grossack’s Blog. Disponível em: https://grossack.site/2021/11/16/dense-pythagorean-triples.html

Referências Matemáticas

Artigos Acadêmicos e Pesquisa

Recursos Educacionais

Aplicações e Contexto Moderno

Discussões Matemáticas

Mathematics Stack Exchange. “Density of Pythagorean triples”. Disponível em: https://math.stackexchange.com/questions/909954/density-of-pythagorean-triples

Inteligência artificial utilizada

Este artigo foi desenvolvido em colaboração com Claude Sonet 3.5 (Anthropic, 2025) https://claude.ai/, dentro do Visual Studio Code (Microsoft, 2025) https://code.visualstudio.com/ para gerar e aprimorar os códigos em Python.

Siga-nos