



Next: Lista 3
Up: Lista 1
- 1.
- Uma onda incidente
está
polarizada
na direção
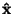 .
Mostre, usando
as condições
de
contorno
dos
campos
elétrico
e magnético,
que
as
ondas
refletida
e
transmitida
também
estão
polarizadas
na
direção
da
onda
incidente.
.
Mostre, usando
as condições
de
contorno
dos
campos
elétrico
e magnético,
que
as
ondas
refletida
e
transmitida
também
estão
polarizadas
na
direção
da
onda
incidente.
- 2.
- Suponha
que
Aeiax + Beibx = Ceicx,
para
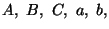 e c constantes
não nulas e para qualquer x.
Mostre que
a=b=c e A+B=C.
e c constantes
não nulas e para qualquer x.
Mostre que
a=b=c e A+B=C.
- 3.
- Qual
a
menor
espessura
de
deposição
de uma camada
de prata
a
ser usada
quando
uma
onda
de
frequência
1010 Hz
incide
sobre
esta
superfície?
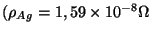 m)
m)
- 4.
- (a)
- Mostre
que
o
comprimento
de
atenuação
de um mal
condutor
é
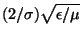 .
Encontre o
comprimento de atenuação
da água,
.
Encontre o
comprimento de atenuação
da água,
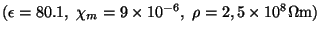 .
.
- (b)
- Mostre
que
o
comprimento
de
atenuação
de um bom
condutor
é
 .
Encontre o
comprimento de atenuação
de um metal típico
.
Encontre o
comprimento de atenuação
de um metal típico
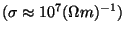 para
para 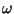 na região do visível,
assuma
na região do visível,
assuma
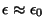 e
e
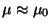 .
.
- (c)
- Mostre
que em
um bom
condutor
o
campo
magnético
está
atrasado
de
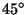 em
relação
ao campo
elétrico
e
encontre
a
razão
de
suas
amplitudes.
Faça
um
exemplo
numérico
usando
o
metal
do
itém
anterior.
em
relação
ao campo
elétrico
e
encontre
a
razão
de
suas
amplitudes.
Faça
um
exemplo
numérico
usando
o
metal
do
itém
anterior.
- 5.
- (a)
- Calcule
a
média
temporal
da
densidade
de
energia
de uma
onda
eletromagnética
plana
em um
meio
condutor.
Mostre
que
a
contribuição
magnética
sempre
domina.
[ Resp.:
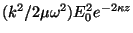 ]
]
- (b)
- Mostre que a intensidade é

- 6.
- Calcule
o coeficiente
de reflexão
para
a
luz
em
uma
interface
ar
para
prata
na
frequência
óptica,
 s.
s.

- 7.
- Encontre
a
largura
da
região
de
dispersão
anómala
no
caso
de
uma
única
ressonância
de
frequência
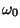 .
Assuma
.
Assuma
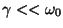 .
Mostre
que
o
índice
de
refração
assume
seus
valores
máximo
e
mínimo
nos
pontos
onde
o
coeficiente
de
absorção
é
metade do
valor
máximo.
.
Mostre
que
o
índice
de
refração
assume
seus
valores
máximo
e
mínimo
nos
pontos
onde
o
coeficiente
de
absorção
é
metade do
valor
máximo.
- 8.
- Assumindo
um
amortecimento
desprezível,
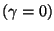 ,
calcule
a
velocidade de
grupo
,
calcule
a
velocidade de
grupo
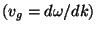 das
ondas
descritas
por
das
ondas
descritas
por
Mostre que vg<c,
mesmo
quando
v>c.
- 9.
- Para um
guia
de
ondas,
- (a)
- determine
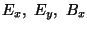 e
By em
termos
das
derivadas parciais
de
Ez e Bz.
e
By em
termos
das
derivadas parciais
de
Ez e Bz.
- (b)
- Mostre que
- 10.
- Para
ondas
MT em um
guia
de ondas
retangular,
determine:
o
campo
elétrico
longitudinal,
as frequências
de
corte,
as
velocidades
da
onda
e
de
grupo.
- 11.
- Mostre
que
para
uma
linha
de transmissão
coaxial
satisfazem as
equações de Maxwell e as condições de contorno para um guia de onda.
Determine
a densidade de carga
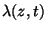 ,
e a
corrente
I(z,t),
equivalentes
no
condutor
interno.
,
e a
corrente
I(z,t),
equivalentes
no
condutor
interno.
- 12.
- Considere as
distribuições
de
carga
e
corrente
que
dão
origem
aos
potenciais
(o exemplo feito em aula).
Considere
agora
uma
caixa
retangular de
comprimento
l,
largura
w,
e altura
h,
situada
a
uma
distância
d acima do plano
yz.
- (a)
- Encontre
a energia
na caixa
em
t1 = d/c,
e em
t2 = (d+h)/c.
- (b)
- Encontre o vetor de
Poynting,
e
determine
o
fluxo
de
energia
por
unidade de
tempo
na
caixa
durante
o
intervalo
t1<t<t2.
- (c)
- Integre
o resultado
anterior
de
t1 até t2e confirme
o resultado
do primeiro
itém.
- 13.
- Encontre
os
campos,
as
distribuições
de
carga
e
corrente
correspondentes
a
- 14.
- Suponha
V=0 e
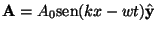 ,
onde
,
onde
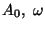 e
k são
constantes.
Encontre
E
e
B,
verifique que
satisfazem as
equações
de
Maxwell no
vácuo.
Que condições
precisam
ser impostas
a
e
k são
constantes.
Encontre
E
e
B,
verifique que
satisfazem as
equações
de
Maxwell no
vácuo.
Que condições
precisam
ser impostas
a
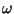 e
k?
e
k?
- 15.
- Use
a
função
de
padrão
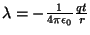 para
transformar
os potenciais no
problem
13
e
comente
os
resultados.
para
transformar
os potenciais no
problem
13
e
comente
os
resultados.




Next: Lista 3
Up: Lista 1
Silvio A. Vitiello
2000-06-19
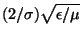 .
Encontre o
comprimento de atenuação
da água,
.
Encontre o
comprimento de atenuação
da água,
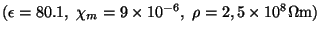 .
.
 .
Encontre o
comprimento de atenuação
de um metal típico
.
Encontre o
comprimento de atenuação
de um metal típico
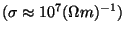 para
para 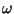 na região do visível,
assuma
na região do visível,
assuma
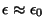 e
e
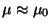 .
.
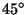 em
relação
ao campo
elétrico
e
encontre
a
razão
de
suas
amplitudes.
Faça
um
exemplo
numérico
usando
o
metal
do
itém
anterior.
em
relação
ao campo
elétrico
e
encontre
a
razão
de
suas
amplitudes.
Faça
um
exemplo
numérico
usando
o
metal
do
itém
anterior.
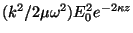 ]
]

![\begin{displaymath}\tilde k= {\omega\over c} \sqrt{\tilde\epsilon_r}
\cong
{\ome...
...{2m\epsilon_0}}\sum_j
{f_j\over{\omega_j^2-\omega^2}}
\right].
\end{displaymath}](s3img21.gif)
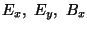 e
By em
termos
das
derivadas parciais
de
Ez e Bz.
e
By em
termos
das
derivadas parciais
de
Ez e Bz.
![\begin{displaymath}\left[
{\partial^2\over\partial x^2}
+
{\partial^2\over\parti...
...\omega\over c})^2
-
Kz
\right]
{E_z\atopwithdelims\{\} B_z}
=0
\end{displaymath}](s3img23.gif)