



Next: Notas
Up: Lista 2
- 1.
- Os
potenciais
dos exs. 13 e 14
da lista 2 estão
no padrão de
Coulomb?
E no padrão
de Lorentz?
- 2.
- Mostre
que é
sempre
possível
escolher
- (a)
-
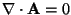
- (b)
-

- (c)
- V = 0
- (d)
- Por que nem sempre podemos escolher
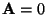
- 3.
- Uma espira como a da figura,
transporta uma corrente que cresce linearmente com o tempo:
I(t) = k t.
- (a)
- Calcule o potencial
vetor
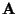 retardo em
O.
retardo em
O.
- (b)
- Encontre o
campo elétrico neste
ponto
assumindo que
o condutor seja
eletricamente neutro.
- (c)
- Por que
este campo não
é nulo?
- 4.
- Suponha
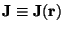 (constante
no tempo) e
(constante
no tempo) e
![$\rho({\bf r} , t) = \rho({\bf r},0) +
[{\partial \rho({\bf r},t)\over{\partial t}}]_{t=0} t$](s4img7.gif) .
Calcule
.
Calcule
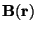 e mostre que
e mostre que
- 5.
- Para correntes que variam lentamente
no tempo podemos
escrever
Mostre que neste caso
- 6.
- Uma partícula
de carga
q move-se
em um
círculo
de
raio
a a uma
velocidade
angular
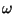 constante.
O círculo está
no plano (x,y),
centrado na
origem
e no
instante
t=0 a
carga esta
em (a,0).
Determine
os potenciais de
Liénard-Wiechert
para
os pontos
do eixo z.
constante.
O círculo está
no plano (x,y),
centrado na
origem
e no
instante
t=0 a
carga esta
em (a,0).
Determine
os potenciais de
Liénard-Wiechert
para
os pontos
do eixo z.
- 7.
- Mostre que o
potencial
escalar
de uma carga puntual
movendo-se com
velocidade
constante
pode
ser
escrito
como
onde
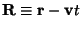 é
o vetor da
posição presente
da partícula
ao ponto
é
o vetor da
posição presente
da partícula
ao ponto
r
onde estamos
calculando o potencial
e 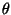 é
o ângulo
entre
é
o ângulo
entre
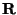 e v.
e v.
- 8.
- Calcule os
campos
elétrico e
magnético
de uma carga puntual
movendo-se
com
velocidade
constante.
- 9.
- Suponha uma carga
q movendo-se
na direção x com uma
aceleração
a.
Calcule os
campos
elétrico e
magnético
para pontos
à direita
e
à esquerda
da carga.
- 10.
- Para
o
mesmo
sistema
do problema
6,
encontre os
campos
elétrico e
magnético
para pontos
no
centro
do
círculo.
A partir
do resultado
para
B,
determine o
campo
magnético
no
centro
de uma
espira
circular
que
transporta
uma
corrente
estacionária
I.
- 11.
- Verifique
que os
potenciais
de um dipolo
oscilante,
satisfazem a
condição do
padrão de
Lorentz.
- 12.
- Encontre a
resistência de
radiação do
fio
que
une
as
duas
extremidades
do dipolo oscilante.
(Esta é a resistência
que
daria a
mesma perda de
potência na forma de calor
que
o dipolo de fato
está perdendo
na forma de radiação.
Expresse
sua resposta
em termos de
um comprimento
de radiação
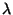 .
Para os fios
de
um rádio
comum,
digamos
com
um
comprimento de
5 cm e
.
Para os fios
de
um rádio
comum,
digamos
com
um
comprimento de
5 cm e
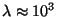 m,
é importante
levarmos em
conta
a
contribuição
radiativa
a
resistência
total?
m,
é importante
levarmos em
conta
a
contribuição
radiativa
a
resistência
total?
- 13.
- Calcule os
campos
elétrico e
magnético
de um
dipolo
magnético
oscilante
diretamente
a
partir de
Calcule o
vetor de Poynting
e mostre
que a
intensidade
de
radiação
obtida
concorda
com
aquela
determinada
em aula.




Next: Notas
Up: Lista 2
Silvio A. Vitiello
2000-06-19
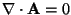

![\includegraphics*[angle=-90,scale=0.7]{esp.ps}](s4img4.gif)
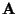 retardo em
O.
retardo em
O.